Persamaan Garis Lurus[sunting | sunting sumber]
Persamaan Garis Melalui 2 Titik[sunting | sunting sumber]
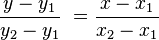
dimana
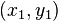 dan
dan 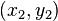 adalah koordinat dari 2 titik
adalah koordinat dari 2 titikPersamaan Garis Melalui 1 Titik Dan Diketahui Gradien[sunting | sunting sumber]
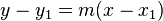
dimana m adalah gradien dari suatu persamaan garis dan
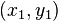 adalah koordinat dari suatu titik
adalah koordinat dari suatu titikGradien Garis[sunting | sunting sumber]
Gradien Oleh 2 Titik[sunting | sunting sumber]
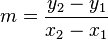
dimana m adalah kemiringan suatu garis dan kedua titik adalah suatu titik yang akan dihitung kemiringannya
Gradien Oleh Persamaan Garis[sunting | sunting sumber]
Bentuk Baku : 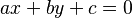
 (a dan b ≠ 0)
(a dan b ≠ 0)
dimana m adalah gradien yang akan dicari dan, 'a' dan 'b' adalah koefisien dari suatu persamaan
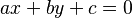
 (a dan b ≠ 0)
(a dan b ≠ 0)dimana m adalah gradien yang akan dicari dan, 'a' dan 'b' adalah koefisien dari suatu persamaan
Gradien Garis Umum[sunting | sunting sumber]
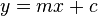
dimana m adalah kemiringan garis
Hubungan Dua Buah Garis[sunting | sunting sumber]
Garis Sejajar[sunting | sunting sumber]
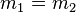
maksud dari dua buah garis sejajar adalah dua buah persamaan yang gradiennya sama
Contoh :
Buktikan
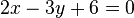 sejajar dengan
sejajar dengan 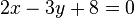 !
!Persamaan 1 :
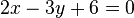 memiliki gradien
memiliki gradien  =
=  .
.Persamaan 2 :
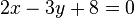 memiliki gradien
memiliki gradien  =
=  .
.Terbukti bila gradien persamaan 1 dan 2 sama, jadi
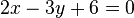 sejajar dengan
sejajar dengan 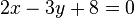
Garis Tegak Lurus[sunting | sunting sumber]
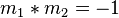
maksud dari dua buah garis tegak lurus adalah dua buah persamaan yang gradiennya terbalik
Contoh :
Buktikan
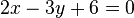 tegak lurus dengan
tegak lurus dengan 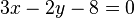 !
!Persamaan 1 (Utama) :
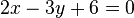 memiliki gradien
memiliki gradien  =
=  .
.Persamaan 2 :
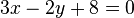 memiliki gradien
memiliki gradien 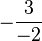 =
=  .
.Lalu kalikan kedua gradien itu
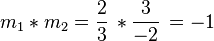 . Terbukti bila
. Terbukti bila 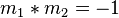 , jadi
, jadi 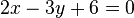 tegak lurus dengan
tegak lurus dengan 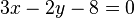
Jarak 2 Buah Titik Dan Garis[sunting | sunting sumber]
Jarak 2 Titik 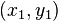 dan
dan 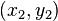 [sunting | sunting sumber]
[sunting | sunting sumber]

Jarak Titik dan Garis[sunting | sunting sumber]
Jarak antara garis : 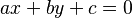 dan titik
dan titik 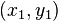

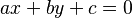 dan titik
dan titik 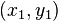

Tidak ada komentar:
Posting Komentar